Solve By Using the Quadratic Equation Lessons
The quadratic formula gives us an alternative to Completing the Square when we cannot factor an equation. People often find the Quadratic Formula method easier and more convenient because it does not require many operations on the equation being solved.
For solving an equation in the variable x, the Quadratic Formula is:

To find the solutions to an equation, we simply need to identify what a, b, and c are, then substitute them into this formula, and simplify.
First Example (Two Solutions)
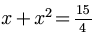
We begin applying the Quadratic Formula by putting the equation in the following form:

Where a, b, and c are constants
This means that each term in the equation must be on the left side, just like when we are factoring or Completing the Square. So we subtract
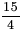 from each side.
from each side.

Now for consistency, we will rearrange the terms so that they are in the same order: The x2 term first, the x term second, and the constant term last.
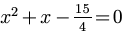
Now by comparing our equation with “ax2 + bx + c = 0″, we can see that a must equal 1, b must equal 1, and
c must equal  .
.

Now that the values of a, b, and c have been determined, we may return to the quadratic formula and use substitution. (Remember to use parentheses when substituting to avoid problems with negative signs.)
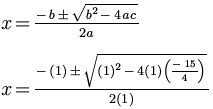
We must now simplify this equation keeping the Order of Operations in mind. We begin by simplifying (1)2.
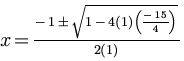
Next, we simplify multiplication. We see that 11 is equal to 15:

Now 1 and 15 are added, resulting in 16.
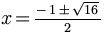
The square root of 16 is 4.
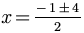
You may recall that the methods of solving by factoring and solving by completing the square required you to split each problem into multiple subproblems to obtain multiple solutions. Since we are again looking for more than one solution, we must split
this problem in two.
So far, we have been carrying the ± sign through the problem. Now, we will create two problems, one with a plus sign, and one with a minus sign.

and
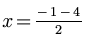
Simplifying the first subproblem gives

Simplifying the second subproblem gives

We can now combine these two solutions into the solution to the original example problem:
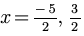
Second Example: One Repeated Solution
Examine the following problem.
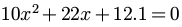
We are using decimal numbers in place of fractions here, but this is a matter of choice. Using decimal numbers will not require us to use the Quadratic Formula any differently.
In this case, the equation is already in the correct format. Using “ax2 + bx + c = 0,” we must now determine a,
b, and c.
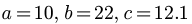
Now we can substitute into the Quadratic Formula:
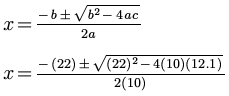
Now we begin simplifying by replacing (22)2 with 484.

Simplifying multiplication, we see that -4(10)(12.1) is equal to -484, and 2(10) is equal to 20.

Notice that we cannot create two different subproblems because +0 and -0 are the same value. Therefore, we simply drop the ±0 from the problem.

Without the two subproblems, we will only have one solution.
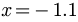
Imaginary and Complex Solutions
Consider the following problem.
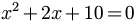
We can identify that
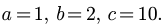
Now, substituting this into the Quadratic Formula:

Simplifying the expression under the radical gives:

Notice that there is a negative number under the square root symbol. If you are familiar with imaginary numbers, you know that the square root of a negative number is an imaginary number, which will cause the solutions to this example to also be imaginary
or complex numbers.
In this lesson, we chose to expose you to this situation, but not to provide details on imaginary and complex solutions. We will add a lesson on this topic after we have introduced imaginary and complex numbers.
Deriving the Quadratic Formula
A more general form of algorithm for finding roots of quadratic equations by completing squares leads to the derivation of what in known as the Quadratic Formula. This is a general formula which can be used to solve for the roots of any quadratic equation.
Given a quadratic equation
then the roots of the equation can be found by completing the square as below:
This can be further simplified as follows
Putting everything under the
under one denominator results in
The above equation is known as the Quadratic Formula.
From this derivation, we can generalize a few equalities based on the formula.
For all real numbers b and c,
For all real numbers b and c,
For all real numbers a, b, and c where a does not equal 0,
The Discriminant of the Quadratic Formula
The part of the quadratic formula under the radical sign is referred to as the discriminant. This is because this expression
is what determines if the quadratic equation whose roots we’re trying to find has real roots, imaginary (complex) roots, or has the same root repeated.
is important because this expression is under the square root sign. Remember that the square root of a number greater than zero (a positive number) is a real number, the square root of zero is zero and the
square root of a number less than zero (a negative number) is an imaginary or complex number. Thus the value of
says a lot about the nature of the roots of the quadratic equation.
-
If
i.e.
This quadratic equation is said to have one repeated root. For example:
looking at only
The above would indicate that the equation has one repeated root, and we already saw that it does indeed have one repeated root.
The roots of the equation are given by x = {-2,-2} which is the same root repeated.
-
If
then
is greater than zero and the quadratic equation whose roots we’re finding is said to have real roots. For example, if asked to find the roots of the given quadratic equation
looking at only
and 1 is greater than zero, we can conclude that the quadratic equation has real roots, which is proved by finding the roots of the equation using the quadratic formula.
and
Therefore the roots of the equation are given by x={-2,-1} which are both real numbers.
-
If
is less than zero and the quadratic equation whose roots we’re finding is said to have complex or imaginary roots. A
complex or imaginary number is denoted by “i“, e.g. 4i is an imaginary number 4.
Given the quadratic equation
, look at only
to find the roots.
which is a negative indicating that the roots of the quadratic equation are imaginary. Knowing this, the roots can be found as follows:
Substituting into the quadratic formula
Since we already know that
is a negative number, we can find the roots by making the following adjustment to the quadratic formula:
notice the i in front of the radical sign indicates that the number is imaginary.
which results in
which gives the roots
Solving Using the Quadratic Formula Resources
|
Practice Problems / Worksheet |
Tutoring
Looking for someone to help you with algebra? At Wyzant, connect with algebra tutors and math tutors nearby. Prefer to meet online? Find online algebra tutors or online math tutors in a couple of clicks.