Completing the Square Lessons
Often, we encounter equations which cannot be easily solved by addition, subtraction, multiplication, division, and factoring. One such equation is

When the highest exponent of an equation is 2, the method of “Completing the Square” gives us an alternative. This method will help us turn this unfactorable equation into an equation that can be factored.
The Strategy
Consider the equation

We can solve this equation by simply taking the square root of each side.

This technique also works when we replace y with an expression like (p – 1):

Solving each of the resulting equations gives p = -2, 4.
The strategy used in completing the square is to get the square of a quantity equal to a number as in

Once this is done, create two subproblems as we did above.
The Process
The completing the square process has five major steps. The summary below assumes that the equation being solved is in the variable x.
- Use addition and subtraction to move the constant term to the right and all other terms to the left.
- Divide each term in the equation by the coefficient of the x
2 term, unless the coefficient is 1. - Determine the coefficient of the x term, divide it by two, square it, and add to both sides.
- Factor the left side as a perfect square trinomial.
- Take the square root of each side, and create two subproblems from the result.
An Example
Let’s begin applying the process to our original example:

Step 1
First, we move the constant term to the right side by adding 1.5 to each side of the equation:

We may now proceed to Step 2 since all other terms are already on the left side of the equation.
Step 2
The coefficient of the x2 term is 1, so we may skip Step 2.
Step 3
We determine that  is the coefficient of the x term. Now we divide this coefficient by two
is the coefficient of the x term. Now we divide this coefficient by two  ,
,
and square it:
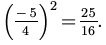 . So we now add
. So we now add  to each side
to each side

Step 4
Now we factor the left side. Even though the left side has fractions, it will always be factorable as x plus half the coefficient of the x term in the original equation (in this case,
 ).
).

Step 5
Finally, we take the square root of each side, and make two subproblems.

Subproblem 1:

Subproblem 2:

As we do with factoring, we combine the solutions to the subproblems to determine the solution to the original problem:

Completing the Square: A Second Example

Step 1
The constant term,  , is already on the right side. But, we must move
, is already on the right side. But, we must move  to the left side. We do this by adding
to the left side. We do this by adding  to each side:
to each side:

Step 2
The coefficient of x2 is 2, so we divide each term in the equation by 2.

Step 3
The coefficient of the x term is  . Dividing
. Dividing  by two, and squaring the result gives
by two, and squaring the result gives  . The next step is to add
. The next step is to add  to each side.
to each side.

Step 4
We must now factor the left side as a perfect square. As in the previous example, we can assume that the factored form is x plus one half the coefficient of x.

Step 5
Finally, we take the square root of each side.

Then create two subproblems:
Subproblem 1:

Subproblem 2:

And combine the solutions to the subproblems in the solution to the original problem:

Completing the Square Quiz
Question 1. In order to ‘complete the square’, what do you do to the ‘middle’ or non-squared x term? (choose 1)
(i.e. x2 + 6x = 15)
Question 2. What do you do with the result from Question #1? (choose 1)
Question 3. When CAN’T you use ‘completing the square’ ? (choose 1)
Completing the Square Resources
|
Completing the Square Calculator Practice Problems / Worksheet
|
Tutoring
Looking for someone to help you with algebra? At Wyzant, connect with algebra tutors and math tutors nearby. Prefer to meet online? Find online algebra tutors or online math tutors in a couple of clicks.